70 Contoh Soal Bangun Ruang Kelas VI/6 SD serta Jawabannya. Lengkap

Assalammualaikum wr.wb. Selamat Pagi semuanya.

Apa kabar sahabat-sahabat semua? Semoga selalu dalam keadaan sehat wal afiat ya serta selalu dalam lindungan dan rahmat- Nya. amin ya rabbal alamin. 

Pada artikel kali ini masharist.com akan membagikan materi tentang BANGUN RUANG.

Artikel ini terdiri dari Rangkuman Bangun Ruang, Contoh Soal dan Pembahasan Luas Permukaan Bangun Ruang, Contoh Soal dan Pembahasan Volume Bangun Ruang serta Contoh Soal Bangun Ruang dan Kunci Jawabannya. Contoh Soal Bangun Ruang terdiri dari Pilihan Ganda dan Essay.

Materi Bangun Ruang ini merupakan materi untuk siswa kelas VI SD. Semoga bermanfaat bagi sahabat-sahabat semua ya.

70 Contoh Soal Bangun Ruang Kelas VI/6 SD serta Jawabannya. Lengkap 

Rangkuman Bangun Ruang

1. Bangun Prisma

Prisma merupakan bangun ruang yang dibatasi oleh  dua sisi. Sisi pertama berbentuk segi banyak, sejajar, dan  kongruen. Sisi lainnya berbentuk persegi panjang. Prisma mempunyai bagian-bagian bangun yang bentuknya berbeda. Segi enam(heksagon) adalah sebuah segibanyak (poligon) dengan enam sisi dan enam titik sudut.

Berikut ini merupakan bagian-bagian dari prisma.

Berikut ini merupakan jaring-jaring prisma.

2. Bentuk Tabung

Tabung atau silinder adalah bangun ruang tiga dimensi yang dibentuk oleh dua buah lingkaran identik yang sejajar dan sebuah persegi panjang yang mengelilingi kedua lingkaran tersebut.Tabung juga bisa disebut prisma segi tak hingga.

Tabung merupakan prisma dengan sisi alas dan sisi atas berbentuk lingkaran. Tabung dapat juga diartikan sebagai bangun ruang, dimana bangun tersebut dibentuk oleh dua lingkaran yang sejajar dan satu persegi panjang yang mengelilingi lingkaran tersebut. 

Bagian-bagian tabung merupakan sisi tabung. Sisi-sisi tersebut terdiri atas sisi alas, sisi tegak atau selimut, dan sisi atas. Sisi alas dan sisi atas tabung berbentuk lingkaran. Selimut tabung berbentuk persegi panjang. Pada tabung ada tinggi, diameter, dan jari-jari tabung.

Berikut ini merupakan bagian-bagian dari tabung

Berikut ini merupakan jaring-jaring tabung

3.   Bangun Limas

Limas adalah bangun ruang yang dibatasi oleh sebuah bangun datar sebagai alas. Selain itu, beberapa buah bidang berbentuk segitiga yang bertemu pada satu titik  puncak. Limas adalah bangun ruang tiga dimensi yang dibatasi oleh alas berbentuk segi-n dan sisi-sisi tegak berbentuk segitiga. 

Limas mempunyai bagian-bagian bangun yang bentuknya berbeda. Berikut ini merupakan bagian-bagian dari limas dan jaring-jaring limas.

limas diberi nama berdasarkan bentuk segi-n pada bidang alasnya. 

4. Bentuk Kerucut

Kerucut merupakan limas dengan sisi alas berbentuk lingkaran. Kerucut dapat juga diartikan sebagai bangun  ruang. Dimana bangun tersebut dibentuk oleh sebuah lingkaran pada sisi alas dan sisi lengkung yang mengelilingi lingkaran tersebut. 

Berdasarkan pengertian titik sudut, kerucut tidak mempunyai titik sudut. Mengapa? Karena kerucut mempunyai titik puncak.

Kerucut mempunyai bagian-bagian. Seperti titik puncak, rusuk, dan sisi. Sisi-sisi sendiri terdiri atas sisi alas dan sisi tegak atau selimut kerucut. Adapun hal-hal yang berkaitan dengan kerucut, yaitu jari-jari, tinggi, dan garis pelukis.

Garis pelukis pada kerucut disebut juga apotema. Panjang garis pelukis (s) biasanya dihitung menggunakan rumus Pythagoras.

Berikut ini merupakan bagian-bagian dari kerucut

Berikut ini merupakan jaring-jaring kerucut

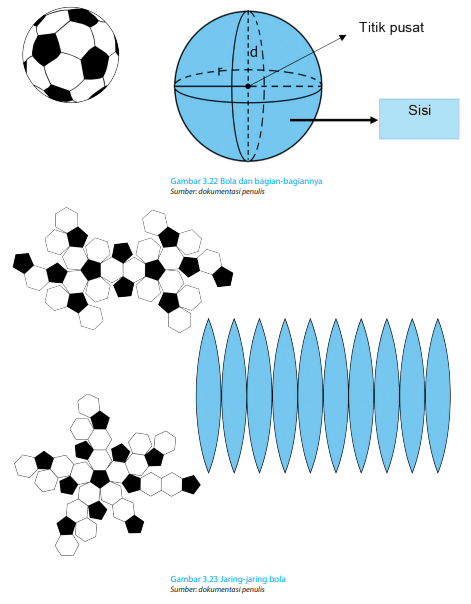
5. Bentuk Bola

 Bola adalah bangun ruang tiga dimensi. Bangun ini dibentuk oleh takhingga lingkaran yang berjari-jari sama panjang. Jari-jari ini berpusat pada satu titik yang sama.

Bola adalah bangun ruang sisi lengkung yang dibatasi oleh satu bidang lengkung. Bola didapatkan dari bangun setengah lingkaran yang diputar satu putaran penuh atau 360 derajat pada garis tengahnya. Bagian dari bangun ruang berbentuk bola disebut sisi. Hal-hal yang berkaitan dengan bola, antara lain jari-jari,diameter, dan titik pusat bola

Berikut ini merupakan bagian-bagian dan jaring-jaring dari Bola

Contoh Soal dan Pembahasan Luas Permukaan Bangun Ruang

Contoh Soal Luas Permukaan dan Pembahasan Prisma Segitiga

1.  Diketahui bahwa alas prisma berbentuk segitiga siku-siku. Ukuran sisi penyikunya 6 cm dan 8 cm. Tingginya 20 cm, seperti gambar berikut. Tentukan Luas Permukaannya.

Jadi, luas alas prisma yang berbentuk segitiga dapat dihitung dengan 

L∆ = ½ x a x t

 = ½ x 8 cm x 6 cm

 = 24 cm²

Sebelum menentukan keliling, hitung sisi yang belum diketahui. Gunakan rumus Pythagoras.

 

c =√( a + b)

= √(6 + 8)

= √(36 + 64)

= √100

= 10

Keliling alas atau keliling segitiga adalah

K∆ = a + b + c

= 8 cm + 6 cm + 10 cm

= 24 cm

Luas permukaan prisma dengan tinggi 20 cm dapat dihitung sebagai berikut.

L = (2 × La) + (K x t)

 = (2 × 24) + (24 × 20)

 = 48 + 480 

 = 528 

Jadi, kertas kado yang dibutuhkan adalah 528 cm².

Contoh Soal Luas Permukaan dan Pembahasan Tabung

1.Diketahui bahwa kaleng mempunyai diameter 8 cm dan tinggi 10 cm. Luas permukaan kaleng 

dapat dihitung dengan cara berikut.

Diameter tabung 8 cm. Jari-jarinya adalah

 r = ½ x d = ½ x 8 cm = 4 cm

 L = 2πr (r + t)

 = 2 x 3,14 x 4 (4 + 10)

 = 2 x 3,14 x 4 x 14

 = 351,68  cm²

Jadi, Luas Permukaan kaleng adalah 351,68 cm²

Contoh Soal Luas Permukaan dan Pembahasan Limas

Contoh Soal Luas Permukaan dan Pembahasan Limas Segi empat

1. Diketahui alas limas berbentuk persegi dengan panjang sisi 6 cm. Luas alas limas dapat dihitung 

dengan cara berikut.

La = s x s 

 = 6 x 6 

 = 36

Jadi luas alas limas adalah 36 cm2

Kamu harus menentukan luas sisi tegak. Hitung lebih dahulu tinggi segitiga menggunakan pythagoras. Perhatikan dengan cermat garis putus-putus. Garis ini membentuk segitiga siku-siku. 

Luas sisi tegak sama dengan luas segitiga. Luas ini dapat dihitung sebagai berikut. 

 L∆ = ½ x a x t

 = ½ x 6 cm x 5 cm

 = 3 x 5

 = 15

Jumlah luas seluruh sisi tegak adalah sebagai berikut.

 Ls = 4 x L∆

 = 4 x 15 

 = 60 

Luas permukaan limas, yaitu

 L = + L∆

 = 36 + 60

 = 96

Jadi, luas pembungkus yang dibutuhkan Siti adalah 96 cm².

Contoh Soal Luas Permukaan dan Pembahasan Kerucut

Diketahui diameter kerucut 6 cm dan garis 15 cm. Diameter lingkaran alas kerucut 6 cm. 

Jari-jarinya adalah

 r = ½ x 6

 = 3 cm

Luas permukaan kerucut dapat dihitung sebagai berikut.

 L = π r (s + r)

 = 3,14 x 3(15 + 3)

 = 3,14 x 3 x 18 

 = 169,56 

Jadi, luas kertas yang dibutuhkannya adalah 169,56 cm²

Contoh Soal Luas Permukaan dan Pembahasan Bola

Diketahui panjang diameter bola 7 cm. Jadi, jari-jari bola tersebut 3,5 cm. Luas permukaan bola adalah 

 L = 4 π r²

 = 4 x 22

7 x 3,5 x 3,5

 = 4 x 11 x 3,5

 = 154

Jadi, luas permukaan bola adalah 154 cm².

Contoh  Soal Gabungan Luas Permukaan Bangun Ruang dan Pembahasannya

1. Tentukan luas permukaan gambar berikut!

Penyelesaian :

Luas sisi tegak limas adalah luas keempat sisi tegak yang berbentuk segitiga. Perhitungannya adalah

 L = 4 x L∆

 = 4 x ½ x 8 x 3

 = 2 x 8 x 3

 = 48 cm²

Luas kubus tanpa tutup adalah luas keempat sisi tegak dan luas alasnya. Perhitungannya adalah

 L = 4 s² + s²

 = (4 x 8 x 8) + (8 x 8)

 = 256 + 64

 = 320 cm²

Luas bangun adalah hasil penjumlahan dari luas sisi tegak limas dan luas kubus tanpa tutup.

 L = 48 +320

 = 368 cm²

Jadi, luas permukaan bangun di atas adalah 368 cm².

2. Ice cream terdiri atas dua bangun ruang yang digabung menjadi satu. Bagian ice cream berbentuk setengah bola. Bangian cone berbentuk kerucut. Panjang diameter ice cream 7 cm dan garis tepi cone 15 cm. Artinya panjang diameter bola dan kerucut 7 cm. Panjang garis pelukis kerucut 15 cm..Perhatikan gambar berikut dengan cermat. Tentukanlah Luas Permukaannya.

Luas permukaan ice cream sama dengan luas permukaan setengah bola. Jika dihitung hasilnya

adalah

 L = x 4 πr²

 = 2πr²

 = 2 x 22/7 x 7/2 cm x 7/2 cm

 = 77 cm²

Luas permukaan cone sama dengan luas permukaan selimut tabung

Ls = π r s

 = 22/7 x 7/2 x 15

 = 165

Luas permukaan bangun adalah jumlah dari luas setengah lingkaran dan luas selimut kerucut.

Hasilnya adalah 

 L = 77 cm² + 165 cm²

= 242 cm²

Jadi, Luas permukaan adalah 242 cm².

Volume Bangun Ruang

Volume Prisma

Misalkan ada 8 tumpukan segitiga. Volume pada Gambar diatas adalah 8 kali luasan segitiga tersebut. Atau dapat dinyatakan sebagai berikut.Volume prisma adalah luas alas bentuk segitiga dikalikan dengan 8 satuan. Jika 8 satuan tinggi prisma, maka volume prisma dapat ditulis 

V = La x t

Keterangan: 

V adalah volume prisma

 La adalah luas alas prisma

 t adalah tinggi prisma

Diketahui panjang sisi segitiga 6 cm. Sebelum menghitung luas, hitung tinggi segitiga. Gunakan r u m u s Pythagoras.

Luas alas prisma adalah

La = L∆ = 1/2 x a x t

 = 1/2 x 6 x 5,2

 = 3 x 5,2 

 = 15,6

Volume prisma dengan tinggi 8 cm adalah

V = La x t

 = 15,6 x 8

 = 124,8

Jadi, volume limas adalah 124,8 cm2

Volume Tabung

Diameter gelas 7 cm dan tinggi gelas 10 cm. Volume tabungnya adalah ?

Luas alas tabung sama dengan luas lingkaran. Misal ada 10 tumpukan. Volume Gambar 3.40 adalah 10 kali luasan lingkaran tersebut. Jika dirumuskan dapat dinyatakan sebagai berikut.

V = La x 10

V = La x t

V = πr2 x t 

Keterangan: 

V adalah volume tabung

 La adalah luas alas tabung berbentuk  lingkaran

 r adalah panjang jari-jari

 t adalah tinggi tabung

.

Diketahui panjang diameter lingkaran 7 cm. Tinggi tabung 10 cm. Volume tabungnya adalah

V = π r² t

 = 22/7 x 7/2 x 7/2 x 10

 = 22/7 x 7/2 x 7/2 x 10

 = 385

Jadi, volume tabung  adalah 385 cm3

Volume Limas

Enam volume limas sama dengan volume kubus

 6 V1 = V2

 6 V1 = s x s x s

 V1 = 1/6 x s x s x s

 V1 = 1/6 x s x s x 2 t

V1 = 1/3 x s x s x t

 V1 = 1/3 x s x s x t

 V1 = 1/3 x La x t

Keterangan : V1 adalah volume limas

 V2 adalah volume kubus

 s adalah sisi kubus

 t adalah tinggi limas

 La adalah luas alas limas

Diketahui panjang sisi alas dan tinggi rumah kaca berbentuk limas segiempat beraturan adalah 6 m, maka volume limas sebagai berikut.

 V = 1/3 x La x t

 = 1/3 x s x s x t

 = 1/3 x 6 m x 6 m x 6 m

 = 72 m3

Jadi, volume rumah kaca adalah 72 m3

Volume Kerucut

V1 = 1/3π r² t

Keterangan : V1 adalah volume kerucut.

 r adalah panjang jari-jari.

 t adalah tinggi kerucut dan tabung

 π adalah konstanta 22/7 atau 3,14

Diameter gelas kotak berukuran 7 cm dan tingginya 6 cm. Volume gelas bentuk kerucut tersebut adalah

 V = 1/3 x π r² t

 = 1/3 x 22/7 x 7/2 x 7/2 x 6 

 =77 

Jadi, volume kerucut adalah 77 cm3

Volume Bola

V = 4/3 π r3

1. Jika diameter akuarium berbentuk bola adalah 21 cm. Volume akuarium adalah

 

V = 4/3 x π r3

 = 4/33 x 22/7 x 21/2 x 21/2 x 21/2 

 = 4.851

Jadi, volume akuarium adalah 4.851 cm3

2. Diketahui sebuah bola dengan volume 4.186,67 liter. Berapa cm jari-jari bola tersebut? (Gunakan π = 3,14)

Penyelesaian

1 liter = 1 dm3

 V = 4/3 π r3

 4.186,67 = 4/3 x 3,14 x r3

 4.186,67 = 12,56 /3 x r3

 4.186,67 : 12,56/3 = r3

 4.186,67 x 3/ 12,56 = r3

 12,560/12,56 = r3

 1.000 = r3

 10 = r

Jadi, jari-jari bola adalah 10 dm atau 100 cm.

Volume Gabungan Bangun Ruang

1. Gambar kapsul terdiri atas dua bangun ruang, yang digabung menjadi satu. Bangun yang membentuk kapsul adalah bangun tabung dan dua bangun setengah bola. Diameter kapsul 7 mm, dan tingginya 15 mm. 

Jari-jari kapsul adalah 

1/2 x 7 = 3,5 mm

Kalian dapat menghitung tinggi tabung dengan cara berikut.

 t = t1 – d

 = 15 – 7

 = 8

Kemudian, volume tabung dicari dengan cara tinggi tabung (t) adalah 8 mm.

 V1 = π r² t

 = 22/7 x 3,5 x 3,5 x 8

 = 308

Volume tabung (V1) adalah 308 mm².

Volume bola dapat dicari dengan cara berikut.

 V2 = 4/3 π r² t

 = 4/3 x 22/7 x 3,5 x 3,5 x 8

 = 180

Volume bola (V2) adalah 180 mm².

Volume kapsul adalah

 V3 = V1 + V2

 = 308 + 180

 = 488

Jadi, volume kapsul adalah 488 mm3

Keterangan

 V1 adalah volume tabung.

V2  adalah volume bola.

V3 adalah volume gabungaan dari bola dan tabung.

t1 adalah tinggi kapsul

Contoh Soal Bangun Ruang Kelas VI/6 SD serta Jawabannya

Pilihan Ganda

1.Andi mempunyai kardus berbentuk kubus yang mempunyai panjang sisi 40 cm. Volume kubus milik Andi adalah …. cm³

a)16.000

b)54.000

c)1.600

d)64.000

2.

Sebuah benda berbentuk kerucut memiliki jari-jari 21 cm dan tingginya 35 cm. Hitunglah volumenya !

a)16.170 cm3

b)15.170 cm3

c)14.160 cm3

d)17.160 cm3

3.

Rino mempunyai kotak pensil berbentuk kubus dengan panjang sisinya 20 cm. Lalu Doni juga punyak kotak pensil berbentuk kubus dengan panjang sisi 15 cm. Selisih volume kotak pensil mereka berdua adalah …. cm³

a)3.375

b)5.225

c)4.625

d)4.425

4.

Rumus untuk mencari volume kubus adalah ….

a)V = s x s x s

b)V = p x l x t

c)V = r x r x r

d)V = s x s

5.

Sebuah Balok adalah bangun ruang yang dibentuk oleh bangun datar ....

a)persegi dan persegi panjang

b)persegi

c)persegi panjang dan segitiga

d)persegi panjang dan lingkaran

6.

Rumus untuk mencari volume balok adalah ….

a)V = P x a x t

b)V = P x l x t

c)V = P x l

d)V = r x a x t

7.

Pilihan paling tepat untuk Rumus volume dan luas permukaan balok ialah ....

a)V = p x l x t , L = 4 (p x l + p x t)

b)V = p x l x t, L = p x l + p x t + l x t

c)V = p x l x t , L = 6 (p x l)

d)V = p x l x t, L = 2 (p x l + p x t + l x t)

8.

Sebuah limas T.ABCD memiliki alas berbentuk persegi panjang dengan panjang AB=CD= 10 cm dan panjang AD=BC= 8 cm. Jika tinggi limas tersebut adalah 12 cm, tentukan volume limas tersebut !

a)190 cm3

b)230 cm3

c)280 cm3

d)320 cm3

9.

Volume tabung gas yang berdiameter 14 cm dan tinggi 25 cm adalah ....

a)4.050 cm3 

b)3.950 cm3 

c)3.850 cm3 

d)3.580 cm3 

10.

Perhatikan gambar!

Yang bukan merupakan jaring-jaring balok adalah gambar ....

a)D

b)C

c)A

d)B

11.

Pak Dani kotak buah berbentuk balok dengan volume sebesar 1.500 dm³. Jika lebar dan tinggi kotak buah itu adalah 100 cm dan 125 cm, maka panjangnya adalah .

a)120 cm

b)140 cm

c)120 dm

d)150 dm

12.

Satu balok memiliki panjang 28 cm, lebar 14 cm, dan tingginya 12 cm. Volume balok tersebut ialah .... cm³

a)4.702

b)4.706

c)4.704

d)4.700

13.

Tentukan Volume gambar A .... cm³

a)6.056

b)6.048

c)6.050

d)6.052

14.

Jaring-jaring kubis diatas, jika alasanya bagian yang disisir, maka atas /tutupnya adalah ...

a)III

b)IV

c)V

d)I

15.

Sebuah kardus berbentuk kubus memiliki volume 32.768 cm. Berapa panjang rusuk tersebut?

a)34 cm

b)31 cm

c)32 cm

d)33 cm

16.

Jumlah rusuk pada bangun kubus sebanyak ….

a)12

b)6

c)14

d)8

17.

Tentukanlah Tinggi sisi gambar B .... cm

a)17

b)18

c)15

d)16

18.

Gambar berikut yang bukan merupakan jaring-jaring kubus adalah ....

a)

b)

c)

d)

19.

Perhatikan gambar!

Volume bangun pada gambar di atas yaitu ... cm³

a)2.200

b)2.210

c)2.100

d)2.110

20.

Diketahui diameter alas tabung 28 cm, tinggi tabung 35 cm. Hitunglah luasnya !

a)4.123 cm2

b)4.213 cm2

c)4.112 cm2

d)4.312 cm2

21.

Hitunglah Lebar sisi gambar C .... cm

a)14

b)9

c)11

d)12

22.

Volume sebuah balok adalah 3.600 cm³. Jika panjang dan tinggi balok tersebut berturut-turut 24 cm dan 10 cm, maka lebarnya ialah .... cm.

a)12

b)18

c)14

d)15

23.

Berikut ini yang merupakan gambar jaring-jaring balok adalah ....

a)

b)

c)

d)

24.

Volume sebuah balok dengan panjang 17 cm, lebar 11 cm, dan tinggi 8 yaitu .... cm³

a)1.498

b)1.516

c)1.502

d)1.496

25.

Luas permukaan balok pada gambar adalah .... cm²

a)1.164

b)1.170

c)1.168

d)1.166

26.

Perbedaan antara balok dan kubus di antaranya adalah ….

a)Jumlah rusuknya

b)Jumlah sisinya

c)Besar sudut-sudutnya

d)Bentuk sisi-sisinya

27.

Ukuran sebuah balok secara berturut-turut yaitu panjang sisinya 16 cm, lebarnya 8 cm, dan tingginya 12 cm.

Luas permukaan balok itu yaitu .... cm²

a)834

b)830

c)832

d)836

28.

Satu buah balok memiliki panjang 23 cm, dan lebarnya 14 cm. Jika volume balok tersebut 5.152 cm³, maka tingginya ialah ... cm.

a)13

b)12

c)16

d)14

29.

Jika D sebagai alas, maka bagian atapnya adalah ....

a)A

b)C

c)B

d)F

30.

Gabungan dari beberapa persegi yang membentuk kubus disebut ...

a)Jaring-jaring tabung

b)Jaring-jaring balok

c)Jaring-jaring limas

d)Jaring-jaring kubus

31.Bola adalah . . . .

a)bangun ruang yang tidak memiliki sisi dan titik sudut

b)bangun ruang yang tidak memiliki sisi

c)bangun ruang yang hanya memiliki satu sisi

d)bangun ruang yang tidak memiliki rusuk dan sisi

32.

Sebuah kaleng roti berbentuk tabung berdiameter 28 cm dan tingginya 10 cm. Volume kaleng roti tersebut adalah .... cm³

a)6.210

b)6.180

c)6.260

d)6.160

33.

Sebuah prisma meliliki alas berbentuk segitiga siku-siku dengan panjang alas 24 cm, tinggi segitiga 10 cm. Jika tinggi prisma 30 cm, maka luas permukaan prisma tersebut .... cm²

a)2.050

b)2.030

c)2.040

d)2.020

34.Berikut ini pernyataan tentang prisma yang paling sesuai adalah . . . .

a)prisma dibatasi oleh bangun datar segitiga

b)prisma mempunyai titik puncak

c)volume prisma adalah sepertiga dari volume limas

d)prisma mempunyai bentuk alas dan bentuk atap yang kongruen

35.Bangun ruang yang mempunyai 18 rusuk, 8 sisi dan 12 titik sudut adalah . . . .

a)limas segienam

b)prisma segienam

c)prisma segilima

d)limas segienam

36.Perhatikan ciri-ciri bangun ruang berikut!

i) mempunyai 5 buah sisi

ii) mempunyai sebagian sisi berbentuk segitiga

iii) mempunyai 5 buah titik sudut

Gambar yang dimaksud berdasarkan ciri-ciri tersebut adalah . . . .

a)

b)

c)

d)

37.

Diketahui sebuah limas memiliki alas berbentuk segitiga dengan panjang 9 cm dan tingginya 12 cm. Jika tinggi limas 15 cm, maka volumenya .... cm³

a)280

b)278

c)270

d)272

38.Diketahui limas tegak dengan alas berbentuk persegi. Jika keliling alas 48 cm dan tinggi limas 8 cm, luas permukaannya adalah ⋯

a)384 cm2

b)483 cm2

c)60 cm2

d)843 cm2

39.

Banyaknya rusuk pada prisma segienam adalah . . . .

a)18

b)7

c)8

d)12

40.

Banyaknya titik sudut pada prisma segienam adalah . . . .

a)18

b)8

c)12

d)7

41.

Luas permukaan bola yang berdiameter 21cm dengan π=22/7 adalah...

a)462 cm2

b)4.851 cm2

c)264 cm2

d)1.386 cm2

42.

Sisi pada bangun ruang tersebut adalah . . . .

a)A, B, C, dan D

b)ABC, ABD, BCD, dan ACD

c)AB, BC, CA, AD, BD, dan CD

d)ABCD

43.

Berikut merupakan ciri-ciri yang benar dari bidang empat adalah . . . .

a)mempunyai 5 titik sudut

b)semua sisinya berbentuk segitiga

c)nama lain daro bidang empat adalah piramida

d)mempunyai 5 buah sisi

44.

Nama lain dari tabung adalah . . . .

a)prisma

b)piramida

c)silinder

d)bidang empat

45.

Berikut ini ciri-ciri yang benar dari tabung kecuali . . .

a)tidak memiliki titik sudut

b)tidak memiliki rusuk

c)memiliki 3 buah sisi

d)mempunyai bentuk alas dan atap berbentuk lingkaran

46.

Bangun ruang yang memiliki satu titik sudut, satu rusuk dan dua buah sisi adalah . . . .

a)bidang empat

b)silinder

c)kerucut

d)tabung

47.

Pernyataan berikut yang benar dari bangun ruang piramida kecuali . . . .

a)memiliki sisi tegak berupa segitiga

b)mempunyai 5 titik sudut

c)disebut juga bidang empat

d)mempunyai 5 buah sisi

48.

Banyaknya sisi pada bangun prisma segilima adalah . . . .

a)10

b)6

c)15

d)7

49.

Panjang diameter alas sebuah kerucut 14 cm. Jika tingginya 24 cm, luas seluruh permukaan kerucut adalah...

a)429 cm2

b)682 cm2

c)704 cm2

d)400 cm2

50.

Perhatikan ciri-ciri bangun ruang berikut!

(i) mempunyai alas dan atap berbentuk segilima

(ii) mempunyai 6 buah titik sudut

(iii) mempunyai 15 buah rusuk

(iv) sisi tegaknya berupa segitiga

Dari pernyataan berikut yang merupakan ciri-ciri prisma segilima adalah . . . .

a)(ii) dan (iii)

b)(i) dan (ii)

c)(i) dan (iii)

d)(ii) dan (iv)

51.

Bangun ruang yang mempunyai sisi tegak berupa segitiga adalah . . . .

a)limas

b)tabung

c)kerucut

d)prisma segitiga

52.

Sebuah tabung diameter alasnya 20 cm (π=3,14) dan tingginya 25 cm. Luas seluruh permukaan tabung adalah...

a)4.396 cm2

b)5.652 cm2

c)2.198 cm2

d)1.570 cm2

53.

Sebuah bangun berbentuk limas, alasnya berbentuk persegi dengan sisi 18 cm. Jika tinggi limas tersebut 20 cm, maka volumenya .... cm³

a)2.170

b)2.164

c)2.160

d)2.150

54.

Sebuah bola mempunyai jari-jari 14 cm. Volume bola itu adalah .... cm³

a)11.526,17

b)11.498,67

c)11.518,57

d)11.514,87

55.

Bangun ruang yang memiliki jumlah sisi sebanyak 7 buah adalah . . . .

a)prisma segilima dan limas segilima

b)prisma segilima dan limas segienam

c)limas segitujuh dan prisma segienam

d)limas segienam dan prisma segitujuh

56.

Sebuah kerucut tingginya 35 cm dan jari-jarinya 15 cm. Volume kerucut tersebut adalah .... cm³

a)8.265

b)8.250

c)8.255

d)8.260

57.

Bangun ruang prisma segitiga mempunyai jumlah rusuk sebanyak . . . .

a)5

b)6 buah

c)9 buah

d)3

58.

Nama lain dari limas segiempat adalah . . . .

a)piramida

b)kubus

c)silinder

d)bidang empat

59.

Sebuah prisma segitiga panjang alasnya 18 cm dan tingginya 15 cm. Jika tinggi prisma 26 cm, maka volumenya .... cm³

a)3.480

b)3.410

c)3.510

d)3.500

60.

Bangun ruang yang tidak memiliki titik sudut dan rusuk adalah . . . .

a)silinder

b)tabung

c)bola

d)kerucut

Essay

61.Sebuah bangun ruang mempunyai sifat-sifat sebagai berikut :

(1) alasnya berbentuk segiempat

(2) memiliki 4 buah sisi yang berbentuk segitiga

(3) memiliki 4 buah rusuk yang sama panjang

(4) mempunyai 1 titik puncak atas.

Bangun ruang yang dimaksud adalah ....

62.Perhatikanlah sifat-sifat bangun ruang berikut.

(1) Mempunyai 5 sisi

(2) Mempunyai 6 titik sudut

(3) Mempunyai 9 rusuk

(4) Sisi tegak berbentuk persegi panjang

Bangun ruang yang memenuhi keempat sifat tersebut adalah...

63.Bangun ruang yang mempunyai alas dan tutup serta selimut adalah ....

64.

(1) mempunyai 6 buah sisi yang berukuran sama

(2) mempunyai 6 buah sisi yang tidak berukuran sama

(3) mempunyai 12 buah rusuk

(4) diagonal rusuknya membentuk 90°

(5) diagonal rusuknya tidak membentuk sudut 90°.

Yang merupakan sifat dari kubus adalah ....

65.

Perhatikanlah sifat-sifat bangun ruang berikut.

(1) Mempunyai 3 rusuk

(2) Mempunyai 2 sisi

(3) Sisi alas berbentuk lingkaran

(4) Sisi tegak berbentuk berbentuk persegi panjang

Sifat-sifat tabung yang benar adalah....

66.

Sebutkan sifat- sifat bangun ruang tabung adalah ....

67.

Perhatikan sifat-sifat bangun ruang berikut ini!

(1) memiliki alas berbentuk lingkaran

(2) memiliki titik puncak

(3) memiliki 2 sisi

(4) memiliki 1 rusuk

(5) memiliki 1 titik sudut

Bangun ruang yang dimaksud adalah ....

68.

Bangun ruang yang sama-sama mempunyai satu titik puncak adalah....

69.

Perhatikan gambar!

Banyak rusuk bangun ruang pada gambar tersebut adalah ....

70.

Perhatikan sifat-sifat bangun ruang berikut!

(1) memiliki 1 sisi

(2) memiliki 1 titik pusat

(3) tidak memiliki titik sudut

(4) memiliki jari-jari tak terhingga dan semuanya sama panjang.

Bangun ruang yang dimaksud adalah ....

Kunci Jawaban/ Answer Key

1.d

2.a

3.c

4.a

5.a

6.b

7.d

8.d

9.c

10.c

11.a

12.c

13.b

14.c

15.c

16.a

17.a

18.c

19.c

20.d

21.b

22.d

23.a

24.d

25.c

26.d

27.c

28.c

29.a

30.d 

31.c

32.d

33.c

34.d

35.b

36.a

37.c

38.a

39.a

40.c

41.d

42.b

43.b

44.c

45.b

46.c

47.c

48.d

49.c

50.c

51.a

52.c

53.c

54.b

55.b

56.b

57.c

58.a

59.c

60.c 

61.Limas segiempat

62.prisma segitiga

63.Tabung

64.(1), (3), (4)

65.3 dan 4

66.

memiliki alas yang berbentuk lingkaran, mempunyai 3 buah sisi, mempunyai 2 buah rusuk, tidak mempunyai titik sudut

67.Kerucut

68.kerucut dan limas

69. 9

70. Bola

Share :